

The work done by the force f acting on the differential area due to the deformation of the differential beam length dx is as follows: The deformation of a differential beam length dx at a distance x from the left-end support is as follows: The stress due to the external loads P1 and P2 on the beam is written as follows:
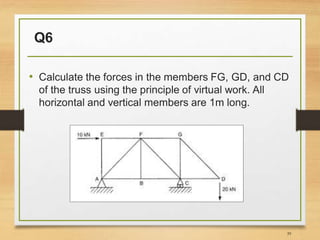
The force acting on the differential area due to the virtual unit load is written as follows: M = internal virtual moment at the section at a distance x e from the left-end support due to the virtual unit load. The stress acting on the differential cross-sectional area dA at a distance x from the left-end support due to a virtual unit load is as follows: First, removing the loads P and W and applying a virtual unit load P v = 1 will cause elementary forces and deformations to develop in the bar, and a small deflection to occur at C, as follows: The deflection at point C due to the applied external loads is required. To develop the equations for the computation of deflection of beams and frames using the virtual work principles, consider the beam loaded as shown in Figure 8.2a. Θ = external rotational displacement caused by real loads.Ĩ.1.1 Virtual Work Formulation for the Deflection and Slope of Beams and Frames Similarly, to obtain the slope at a point on a structure, apply a unit virtual moment M v at the specified point where the slope is desired, and apply the following equation derived via the principle of conservation of energy: ∆ = external displacement caused by real loads.ĭS = internal deformation caused by real loads. The work done by the virtual forces are as follows:Īpplying the principle of conservation of energy by equating equation 8.1 and equation 8.2 suggests the following: Upon placement of the real load, the point of application of the virtual load also displaces by ∆, and the applied unit load performs work by traveling the distance ∆. Then, placing the real external loads P 1, P 2, and M on the same body will cause an internal deformation, dS, and an external deflection of point Q to Q’ by an amount ∆. First, applying a virtual or fictitious unit load P v = 1 at a point Q, where the deflection parallel to the applied load is desired, will create an internal virtual or imaginary load f and will cause point Q to displace by a certain small amount. To illustrate the principle of virtual work, consider the deformable body shown in Figure 8.1. This method was developed in 1717 by John Bernoulli. The virtual work method, also referred to as the method of virtual force or unit-load method, uses the law of conservation of energy to obtain the deflection and slope at a point in a structure. \)ĭeflections of Structures: Work-Energy Methods


 0 kommentar(er)
0 kommentar(er)
